Sorting

Sorting is a very important and fundamental problem in the study of computer algorithms.

When we’re sorting, we start with a list of n items, and when we’re done, we want the list to contain the same items, but rearranged into nondecreasing order. (I’d say “into increasing order,” but two or more items might be equal.)

The list items might be a type that already has a way to order it, such as numbers or strings. But they might be something else, such as references to objects. In general, we can say that each list item has a sort key, which is the part of the item that determines the correct sorted order. In the case of objects, an object might have satellite data that travels with the sort keys. (No, satellite data does not necessarily come from satellites.) For example, when I make the final grades in this course, I will sort. The sort key will be the percentage of available points that you have earned. The satellite data will be your name. (If I sorted only the points and didn’t move the names around, too, then those whose names are at one end of the alphabet all get A’s and those whose names are at the other end don’t do so well.)

Python provides built-in functions to sort items. There’s the sorted function that creates a sorted copy of a list. There’s also a sort method, which sorts a list in place:

But how does sorting work? There are dozens of different sorting algorithms. Although the results of each algorithm are the same (a sorted list), some algorithms are more efficient than others, depending on how the data is initially organized in the list.

It may seem silly to implement a sorting method when Python already has one built-in, but every card-carrying computer scientist knows the basic sorting algorithms. They are to the canon of computer science as The Iliad is to the canon of classical literature—and it takes a lot less time to understand how to sort than it takes to read The Iliad.

We’ve already seen one sorting algorithm: selection sort. Here it is again:

Selection sort looks over the remaining list of items, finds the smallest, and moves that item into place.

Exercise: selection sort cards

Objective: Predict the behavior of a sorting algorithm.

Here are some cards, from the Algorithms tutorials on Khan Academy (for which Balkcom and Cormen are co-authors). You can click on one card, and then another, to swap the locations of the cards. Sort the cards using the selection-sort algorithm.

Insertion sort

The insertion sort algorithm takes a different approach. Insertion sort inspects only the next item, and then inserts that new item into the already-sorted part of the list.

Here is a visualization, from the Algorithms tutorials on Khan Academy (for which Balkcom and Cormen are co-authors):

In insertion sort, we have a list, say the_list, and it’s initialized some values:

the_list = [5, 2, 4, 6, 1, 3]

Consider the sublist containing just the item in the_list[0]. Is this sublist sorted? Of course! Any sublist containing just one item is sorted.

Next, we consider the item in the_list[1]. We are going to figure out where in the sublist to its left it should go. Let’s give the item in the_list[1] the name key, so that key has the value 2. We compare key with the item immediately to the left of the_list[1], namely the_list[0], which has the value 5. We see that key, since it has the value 2, is less than the_list[0], which has the value 5. So we know that key should go somewhere to the left of the item in the_list[0]. We shift the item in the_list[0] over one position to the right, into the_list[1]. At this point, we have hit the left end of the list, and we stop and drop key into the_list[0]. At this point the sublist of the_list starting at index 0 and going through index 1 is sorted, and the_list is [2, 5, 4, 6, 1, 3].

Next, we consider the item in the_list[2], with value 4. Again, we figure out where in the sublist to its left it should go. We set key to 4 and compare it with the item immediately to its left, in the_list[1], with value 5. We see that key is less than the_list[1], and so we know that key will go somewhere to the left of the_list[1]. We shift the item in the_list[1] over one position to the right, into the_list[2]. Next, we compare key with the item in the_list[0]. We see that key is not less than this item, whose value is 2, and so we know that key does not go its left. We stop comparing key with items to its left, and we drop key into the last position out of which we shifted an item, namely the_list[1]. At this point, the sublist of the_list starting at index 0 and going through index 2 is sorted, and the_list is [2, 4, 5, 6, 1, 3].

We repeat this process:

If we look at our example after each item is processed, we see, in order

[5, 2, 4, 6, 1, 3]   # initial list
[2, 5, 4, 6, 1, 3]   # after processing the_list[1]
[2, 4, 5, 6, 1, 3]   # after processing the_list[2]
[2, 4, 5, 6, 1, 3]   # after processing the_list[3]: it's already greater than everything to its left
[1, 2, 4, 5, 6, 3]   # after processing the_list[4]
[1, 2, 3, 4, 5, 6]   # after processing the_list[5]: done

Notice that finding an item equal to key is just as good as finding an item that is less than key. In either case, there’s no need to shift this item to the right, and so we stop marching to the left.

Here is some code for insertion sort.

Exercise: factor insertion sort

Objective: Factor out a function from a section of code.

The code for insertion sort includes an outer loop and an inner loop. The inner loop takes an item, the key, at some index in the list, and slides items one to the right until the correct space has been made available to place the key. Write a function insert that takes as parameters a list and the index of the key, and inserts the key into the correct location. Re-write insertion sort to use insert.

Here is a solution. No peeking until you have solved it yourself!

Merge sort

Next, we’re going to use recursion to sort a list.

We will see later than merge sort is faster than selection sort and insertion sort in what we call the “worst case.” Merge sort is not the sorting algorithm of choice for small problem sizes. Once the problem size is in the range 500–1000, merge sort beats the other two, and its advantage increases as the problem size increases from there.

Another potential disadvantage of merge sort is that it does not work in place. That is, it has to make complete copies of the entire input list. Contrast this feature with selection sort and insertion sort, which at any time keep a copy of only one list entry rather than copies of all the list entries. Thus, if space is at a premium, merge sort might not be the sorting algorithm of choice.

For most occasions, however, merge sort will be just fine.

Linear-time merging

The key to making merge sort work is a linear-time merging step. (By “linear-time,” we mean that the time it takes is proportional to the number of items being merged. We’ll see exactly what that means later.) The idea is follows. Suppose we have two sorted lists, say a[0:m], containing m items in a[0] through a[m-1], and b[0:n], containing n items in b[0] through b[n-1], and we wish to produce a sorted list c[0:m+n] containing all m + n items in either a or b, ending up in c[0] through c[m+n-1].

Here is an important observation: there are only two candidates for the value that should be in c[0] (the smallest item of the output), and these candidates are a[0] and b[0]. Why? Because the lists a and b are sorted, the smallest item overall must be the smallest item of whichever list, a or b, it started in. So we take the smaller of a[0] and b[0] and copy it into c[0].

Let’s say that it turned out that a[0] < b[0], so that we copied a[0] into c[0]. The value that should go into c[1] is the second-smallest item overall, and it is also the smallest item of those remaining in a[1:m] and b[0:n]. Using the same reasoning as before, there are only two candidates for this value: a[1] and b[0]. We pick the smaller of these values and copy it into c[1].

In general, as we are copying values into c, we have to look at only two candidate values: the smallest remaining value in a and the smallest remaining value in b. We can quickly determine which of these values is smaller, to copy it into the correct position of c, and to update any indices into lists a, b, and c.

It would be a very good exercise to write merge yourself, but here is one version. In this version, both of the sorted lists are initially contained within a single list, at indices p…q (for the first sorted list), and q+1…r. So the function merge takes the list, p, q, and r as inputs. After merging, the result is put back into the list at index p, overwriting the original lists.

Notice that we can copy part of one list into another using slice notation, that is the colon within the square brackets. So this line:

the_list[k : r+1] = left[i:]

copies the items in left starting at i into the_list, starting at index k.

The merge function merges the sorted sublists the_list[p : q+1] (containing the items from index p through index q—remember that with slice notation, the index after the colon is 1 greater than the index of the last item in the sublist) and the_list[q+1 : r+1] (containing the items from index q+1 through index r) into the sorted sublist the_list[p : r+1]. Notice that here the lists being merged are actually two consecutive sublists of the_list, and that they are being merged into the same locations, indices p through r, that they started in. The merge function creates two new temporary lists, left and right, copied from the original list. It then merges back into the original list. It repeatedly chooses the smaller of the unmerged items in left and right and copies it back into the_list. The index i always tells us the where to find the next unmerged item in left; j indexes the next unmerged item in right, and k indexes where the next merged item will go in the_list. Eventually, we exhaust either left or right. At that time, the other list still has unmerged items, and we can just copy them back into the_list directly.

Notice that the parameters p and r to merge have default values of 0 and None, respectively. Recall that in Python, None is a special value that means “no value at all.” Here we use it so that if we just call merge_sort(some_list), the code assumes that you want to sort the entire list, by setting p to 0 and r to the last index in the list.

Divide-and-Conquer

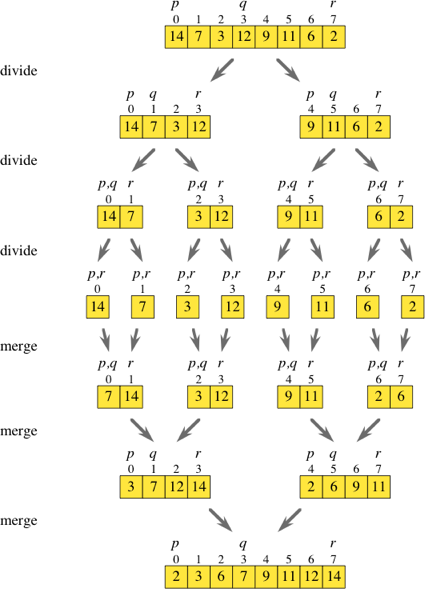
Now that we have the linear-time merging function merge, we need to use it well. Merge sort works by a common computer-science paradigm known as divide-and-conquer:

  1. Divide the problem into (approximately) equal-size subproblems.
  2. Conquer by solving the subproblems recursively.
  3. Combine the solutions to the subproblems to solve the original problem.

For merge sort, the problem to be solved is sorting the sublist the_list[p] through the_list[r]. Initially, for a list with n items, we’ll have p = 0 and r = n–1, but these values will be different for the recursive calls. Merge sort follows the divide-and-conquer paradigm as follows:

  1. Divide by finding the index q of the midpoint of the sublist the_list in ranges p…r, and considering the sublists p…q and (q+1)…r.
  2. Conquer by merge sorting the smaller sublists.
  3. Combine by merging the sorted sublists. r+1]`.

Here’s an example of merge sort in action.

Exercise: merge sort

Objective: implement a recursive sorting algorithm.

Unfold the merge_sort function in the code below by clicking on the small arrow next to the appropriate line number. Complete the merge_sort function by writing the recursive case. You’ll need to compute the midpoint q of the sublist p..r (you have integer variables available), make two recursive calls to merge_sort, and merge the results using the provided merge function.

Here is a solution for merge sort. No peeking until you’ve solved it yourself!

How merge sort runs

The recursion “bottoms out” when the sublist to be sorted has fewer than 2 items, since a sublist with 0 or 1 items is already sorted.

The merge_sort function shows how easy divide-and-conquer is for merge sort. It almost seems like cheating! But if you understand recursion, you’ll believe that it works.

If you don’t understand how the recursion works—I mean really understand it—I recommend that you

Sorting a list of objects

The merge sort function we saw is fine for sorting lists of items that can be easily compared, like strings or ints. What if we wanted to sort a list that contained addresses of (references to) objects? How does Python know which object is “less than” another?

If you are using the Python .sort method, it turns out that you can write a special method __lt__ in the class definition. __lt__ is then used to compare the objects when you use the less-than symbol <.

But here, we’re not using the Python .sort method. We’re writing our own sorting code. How can we specify how we want to compare objects?

Imagine that you have a list of planets. You might wish to sort by mass, by distance from the sun, or by mean orbital velocity. These quantities might be stored in instance variables of a Planet object, or they might be computable using instance variables of a Planet object.

There is only one place in the merge sort code where we compare items from the list:

        if left[i] < right[l]:

We need a function to replace the <. Let’s say we had two Planet objects, each with a mass instance variable. We could write the function like this:

def lessthan_mass(body1, body2):
    return body1.mass < body2.mass

I included “mass” in the function name to make it clear that this “less than” function compares masses. Somehow I need to specify to the merge sort code that merge should use the lessthan_mass function instead of a simple < sign in comparisons. Fortunately, we can pass a function as a parameter to another function. We rewrite the header for merge_sort like this:

def merge_sort(the_list, p, r, compare_fn)

and for merge:

def merge(the_list, p, q, r, compare_fn):

When merge_sort is called, we just pass in lessthan_mass (itself a function) as the second parameter. Within merge_sort, we change the call to merge to include compare_fn as the second actual parameter. Finally, in the body of merge, we can use compare_fn to compare items rather than using the < sign:

        if compare_fn(left[i], right[j]):
◄≡►
Project Python